Highlights & Demo

In this paper we present a new strategy to model the subgrid-scale scalar flux in a three-dimensional turbulent incompressible flow using physics-informed neural networks (NNs). When trained from direct numerical simulation (DNS) data, state-of-the-art neural networks, such as convolutional neural networks, may not preserve well known physical priors, which may in turn question their application to real case-studies. To address this issue, we investigate hard and soft constraints into the model based on classical invariances and symmetries derived from physical laws. From simulation-based experiments, we show that the proposed physically-invariant NN model outperforms both purely data-driven ones as well as parametric state-of-the-art subgrid-scale model. The considered invariances are regarded as regularizers on physical metrics during the a priori evaluation and constrain the distribution tails of the predicted subgrid-scale term to be closer to the DNS. They also increase the stability and performance of the model when used as a surrogate during a large-eddy simulation. Moreover, the physically-invariant NN is shown to generalize to configurations that have not been seen during the training phase. Related paper: Frezat et al. Physical invariance in neural networks for subgrid-scale scalar flux modeling. Arxiv, 2020 (link) Associated code: git

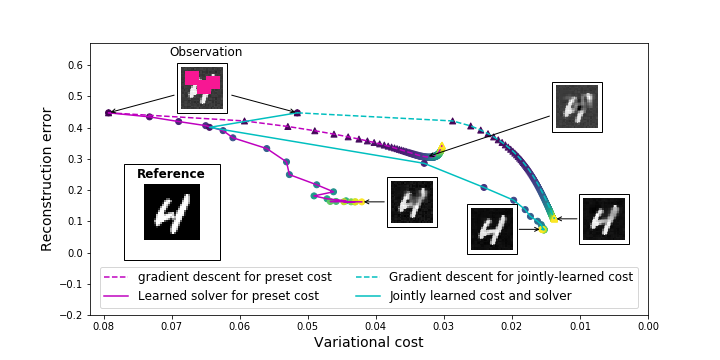Designing appropriate variational regularization schemes is a crucial part of solving inverse problems, making them better-posed and guaranteeing that the solution of the associated optimization problem satisfies desirable properties. Recently, learning-based strategies have appeared to be very efficient for solving inverse problems, by learning direct inversion schemes or plug-and-play regularizers from available pairs of true states and observations. In this paper, we go a step further and design an end-to-end framework allowing to learn actual variational frameworks for inverse problems in such a supervised setting. The variational cost and the gradient-based solver are both stated as neural networks using automatic differentiation for the latter. We can jointly learn both components to minimize the data reconstruction error on the true states. This leads to a data-driven discovery of variational models. We consider an application to inverse problems with incomplete datasets (image inpainting and multivariate time series interpolation). We experimentally illustrate that this framework can lead to a significant gain in terms of reconstruction performance, including w.r.t. the direct minimization of the variational formulation derived from the known generative model. Related paper: Fablet et al. Joint learning of variational representations and solvers for inverse problems with partially-observed data. Arxiv, 2020 (link) Associated code: git

Bridging physics and deep learning is a topical challenge. While deep learning frameworks open avenues in physical science, the design of physicallyconsistent deep neural network architectures is an open issue. In the spirit of physics-informed NNs, PDE-NetGen package provides new means to automatically translate physical equations, given as PDEs, into neural network architectures. PDE-NetGen combines symbolic calculus and a neural network generator. The later exploits NN-based implementations of PDE solvers using Keras. With some knowledge of a problem, PDE-NetGen is a plug-and-play tool to generate physics-informed NN architectures. They provide computationally-efficient yet compact representations to address a variety of issues, including among others adjoint derivation, model calibration, forecasting, data assimilation as well as uncertainty quantification. As an illustration, the workflow is first presented for the 2D diffusion equation, then applied to the data-driven and physics-informed identification of uncertainty dynamics for the Burgers equation. Related paper: Pannekoucke and Fablet. PDE-NetGen 1.0: from symbolic PDE representations of physical processes to trainable neural network representations. Geoscientific Model Development, 2020 (link) Associated code: git

For numerous domains, including for instance earth observation, medical imaging, astrophysics,..., available image and signal datasets often involve irregular space-time sampling patterns and large missing data rates. These sampling properties may be critical to apply state-of-the-art learning-based (e.g., auto-encoders, CNNs,...), fully benefit from the available large-scale observations and reach breakthroughs in the reconstruction and identification of processes of interest. In this paper, we address the end-to-end learning of representations of signals, images and image sequences from irregularly-sampled data, i.e. when the training data involved missing data. From an analogy to Bayesian formulation, we consider energy-based representations. Two energy forms are investigated: one derived from auto-encoders and one relating to Gibbs priors. The learning stage of these energy-based representations (or priors) involve a joint interpolation issue, which amounts to solving an energy minimization problem under observation constraints. Using a neural-network-based implementation of the considered energy forms, we can state an end-to-end learning scheme from irregularly-sampled data. We demonstrate the relevance of the proposed representations for different case-studies: namely, multivariate time series, 2D images and image sequences.Related paper: Ouala et al. Learning Latent Dynamics for Partially-Observed Chaotic Systems. arXiv 2019. (link)

This study addresses the data-driven identification of latent dynamical representations of partially-observed systems, i.e. dynamical systems for which some components are never observed, with an emphasis on forecasting applications, including long-term asymptotic patterns. Whereas state-of-the-art data-driven approaches rely on delay embeddings and linear decompositions of the underlying operators, we introduce a framework based on the data-driven identification of an augmented state-space model using a neural-network-based representation. For a given training dataset, it amounts to jointly learn an ODE (Ordinary Differential Equation) representation in the latent space and reconstructing latent states. Through numerical experiments, we demonstrate the relevance of the proposed framework w.r.t. state-of-the-art approaches in terms of short-term forecasting performance and long-term behaviour. We further discuss how the proposed framework relates to Koopman operator theory and Takens' embedding theorem. Related paper: Ouala et al. Learning Latent Dynamics for Partially-Observed Chaotic Systems. arXiv 2019. (link)

This study addresses the understanding and characterization of residual networks (ResNet), which are among the state-of-the-art deep learning architectures for a variety of supervised learning problems. We focus on the mapping component of ResNets, which map the embedding space toward a new unknown space where the prediction or classification can be stated according to linear criteria. We show that this mapping component can be regarded as the numerical implementation of continuous flows of diffeomorphisms governed by ordinary differential equations. In particular, ResNets with shared weights are fully characterized as numerical approximation of exponential diffeomorphic operators. We stress both theoretically and numerically the relevance of the enforcement of diffeomorphic properties and the importance of numerical issues to make consistent the continuous formulation and the discretized ResNet implementation. We further discuss the resulting theoretical and computational insights into ResNet architectures. Related paper: Rousseau et al. Residual Networks as Flows of Diffeomorphisms. JMIV 2019 (link)

Current generation satellite altimetry missions have played a fundamental role in improving our understanding of sea surface dynamics, despite only being able to provide measurements along the satellite track.In this respect, the future SWOT altimetry mission will be the first mission to produce complete two-dimensional wide-swath satellite observations. With a view towards the upcoming SWOT mission launch, we explore the potential of SWOT observations to improve the reconstruction of high-resolution sea level anomaly (SLA) fields from satellite-derived data. Given the ever-increasing availability of multi-source datasets that supports the exploration of data-driven alternatives to classical model-driven formulations, we focus here on recently introduced data-driven models for the interpolation of geophysical fields. Using an Observing System Simulation Experiment (OSSE), we demonstrate the relevance of SWOT observations to better constraint data-driven interpolation models in order to improve the reconstruction of mesoscale features. Reported results suggest that SWOT observations can provide more information than currently available nadir along-track altimetry observations and show an additional SLA reconstruction performance improvement when the joint assimilation of SWOT and nadir along-track observations is considered. Related paper: Lopez Radcenco et al., Analog Data Assimilation for Along-track Nadir and SWOT Altimetry Observations in the Western Mediterranean Sea. IEEE JSTARS, 2019 (link)

The forecasting and reconstruction of oceanic dynamics is a crucial challenge. While model driven strategies are still the state-of-the-art approaches in the reconstruction of spatio-temporal dynamics. The ever increasing availability of data collections in oceanography raised the relevance of data-driven approaches as computationally efficient representations of spatio-temporal fields reconstruction. This tools proved to outperform classical state-of-the-art interpolation techniques such as optimal interpolation and DINEOF in the retrievement of fine scale structures while still been computationally efficient comparing to model based data assimilation schemes. However, coupling this data-driven priors to classical filtering schemes limits their potential representativity. From this point of view, the recent advances in machine learning and especially neural networks and deep learning can provide a new infrastructure for dynamical modeling and interpolation within a data-driven framework. In this work we adress this challenge and develop a novel Neural-Network-based (NN-based) Kalman filter for spatio-temporal interpolation of sea surface dynamics. Based on a data-driven probabilistic representation of spatio-temporal fields, our approach can be regarded as an alternative to classical filtering schemes such as the ensemble Kalman filters (EnKF) in data assimilation. Overall, the key features of the proposed approach are two-fold: (i) we propose a novel architecture for the stochastic representation of two dimensional (2D) geophysical dynamics based on a neural networks, (ii) we derive the associated parametric Kalman-like filtering scheme for a computationally-efficient spatio-temporal interpolation of Sea Surface Temperature (SST) fields. We illustrate the relevance of our contribution for an OSSE (Observing System Simulation Experiment) in a case-study region off South Africa. Our numerical experiments report significant improvements in terms of reconstruction performance compared with operational and state-of-the-art schemes (e.g., optimal interpolation, Empirical Orthogonal Function (EOF) based interpolation and analog data assimilation). Related paper: Ouala et al. Neural Network Based Kalman Filters for the Spatio-Temporal Interpolation of Satellite-Derived Sea Surface Temperature. Remote Sensing, 2018 (link)

Satellite-derived products are of key importance for the high-resolution monitoring of the ocean surface at a global scale. Due to the sensitivity of spaceborne sensors to the atmospheric conditions as well as the associated spatio-temporal sampling, ocean remote sensing data may involve high-missing data rate. The spatio-temporal interpolation of these data remains a key challenge to deliver L4 gridded products to end-users. Whereas operational products mostly rely on model-driven approaches, especially optimal interpolation based on Gaussian process priors, the availability of large-scale observation and simulation datasets advocate for the development of novel data-driven models. This study investigates such models. We extend the recently introduced analog data assimilation to high-dimensional spatio-temporal fields using a multi-scale patch-based decomposition. Using an Observing System Simulation Expriment (OSSE) for sea surface temperature, we demonstrate the relevance of the proposed data-driven scheme for the real missing data patterns of the high-resolution infrared METOP sensor. It resorts to a significant improvement w.r.t. state-of-the-art techniques in terms of interpolation error (about 50 % of relative gain) and spectral characteristics for horizontal scales smaller than 100km. We further discuss the key features and parameterizations of the proposed data-driven approach as well as its relevance with respect to classical interpolation techniques. Related paper: Fablet et al. Data-driven Models for the Spatio-Temporal Interpolation of satellite-derived SST Fields. IEEE TCI 2017 (link) Associated code: git

In light of growing interest in data-driven methods for oceanic, atmospheric, and climate sciences, this work focuses on the field of data assimilation and presents the analog data assimilation (AnDA). The proposed framework produces a reconstruction of the system dynamics in a fully data-driven manner where no explicit knowledge of the dynamical model is required. Instead, a representative catalog of trajectories of the system is assumed to be available. Based on this catalog, the analog data assimilation combines the nonparametric sampling of the dynamics using analog forecasting methods with ensemble-based assimilation techniques. This study explores different analog forecasting strategies and derives both ensemble Kalman and particle filtering versions of the proposed analog data assimilation approach. Numerical experiments are examined for two chaotic dynamical systems: the Lorenz-63 and Lorenz-96 systems. The performance of the analog data assimilation is discussed with respect to classical model-driven assimilation. Related paper: Lguensat et al. The Analog Data Assimilation. Monthly Weather Review, 2017 (link) Associated code: git